js实现前端常用的几种排序的算法逻辑
创建时间:2020-09-22 更新时间:2020-09-22算法主要用于对一个值的初始状态经过一系列的计算得到新的状态。
算法不分前后端,只是在前端中的使用场景很少,特别是做后台管理系统一类的项目。接触算法能让自己的逻辑思维能力变得更稠密、清晰,提高对逻辑复杂的代码块的阅读能力。
排序算法是大部分程序员入门最早接触的算法,目前多达10+种,我选择了下表所示的3种,用js的语法来实现它们的逻辑:
| 排序算法名称 | avg时间复杂度 | min时间复杂度 | max时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n) | O(n2) | O(1) | 稳定 |
| 快速排序 | O(n log(n)) | O(n log(n)) | O(n2) | O(log(n)) | 不稳定 |
| 归并排序 | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) | 稳定 |
冒泡排序(Bubble)
冒泡是我读书上Java课学到的,最简单、易理解,其核心的思路是:
遍历整个数组,依次两两相邻比较,满足condition则互换,每次循环确定1个数。
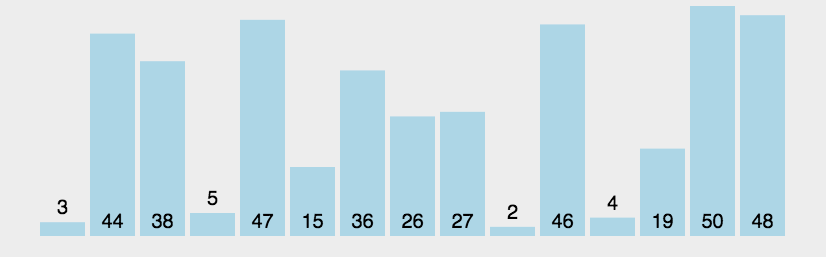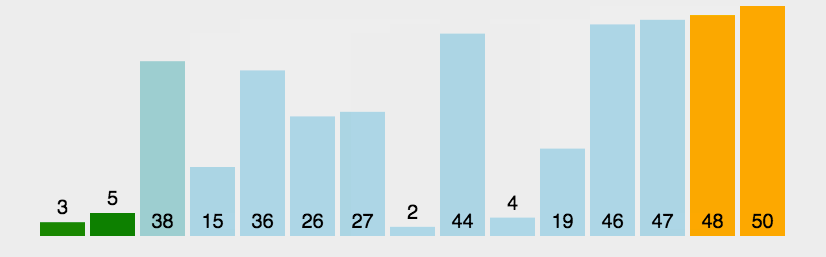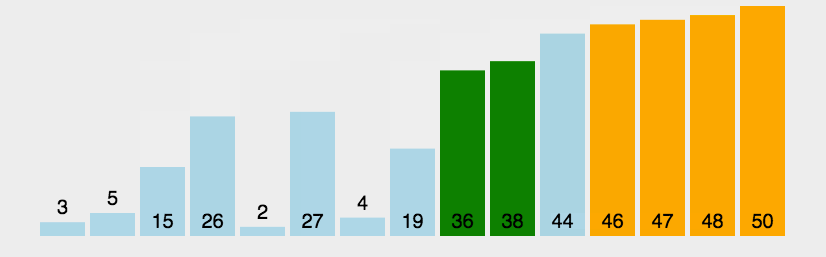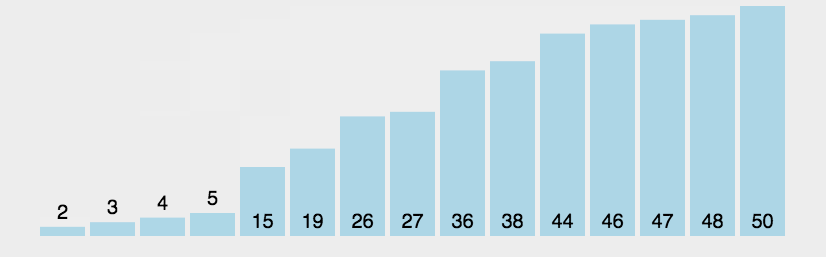
function bubbleSort(arr) {
for (let i = 0, l = arr.length; i < l; i++) {
for (let j = 0, m = l - i - 1; j < m; j++) {
if (arr[l - j - 2] > arr[l - j - 1]) {
let temp = arr[l - j - 2]
arr[l - j - 2] = arr[l - j - 1]
arr[l - j - 1] = temp
}
}
}
}可以看到,上图所示,是头到尾的遍历,我的代码是从尾到头的,只是为了体现出往前冒泡的感觉,没有差异。
快速排序(Quick)
JS中的 Array.prototype.sort() ,不同浏览器实现的方法不同,对于Chrome,源码显示,当数组长度小于10时用插入排序,否则用快速排序。
快排是一种先整后分的分治的概念,非常适用于数据量大的场景,其核心的思路是:
选取一个基准值,其余值依次跟它比较,小于基准值的放左边,大于等于基准值的放右边,基准值放中间,完成第一次排序,然后左右数组各自递归,最终完成排序。
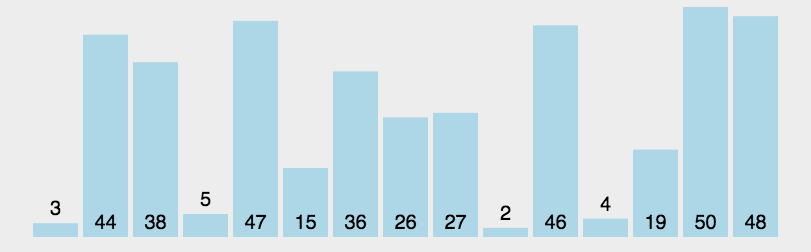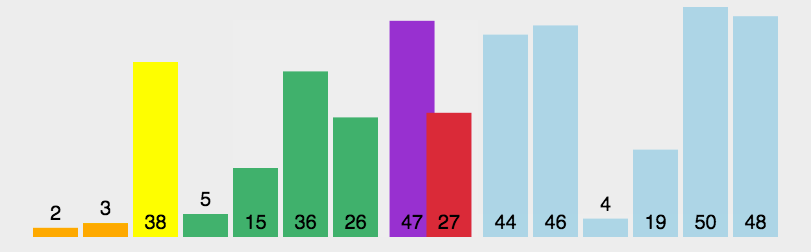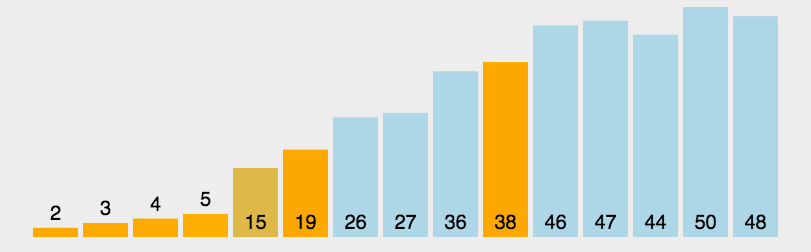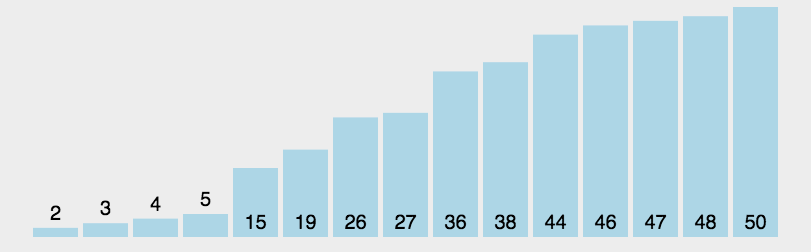
function quickSort(arr, start = 0, end = arr.length - 1) {
if (end <= start) return
let temp = [arr[start]]
let mid = start
for (let i = start + 1; i <= end; i++) {
if (arr[start] > arr[i])) {
temp.push(arr[i])
} else {
temp.unshift(arr[i])
mid++
}
}
for (let i = 0; i < temp.length; i++) {
arr[start + i] = temp[i];
}
quickSort(arr, start, mid - 1)
quickSort(arr, mid + 1, end)
}归并排序(Merge)
归并也是分治的概念,它有两种实现的方法:自上而下的递归、自下而上的迭代,我用的是自上而下递归。
归并的分治和快排的分治不同,快排是边排边拆,再分开递归,而归并则是先拆后排(先拆后合),其核心的思路是:
将数组对半分,分开递归一直对半分,直到全部拆成单个,然后顺着拆分的树,左右像打车轮战一样完成排序。
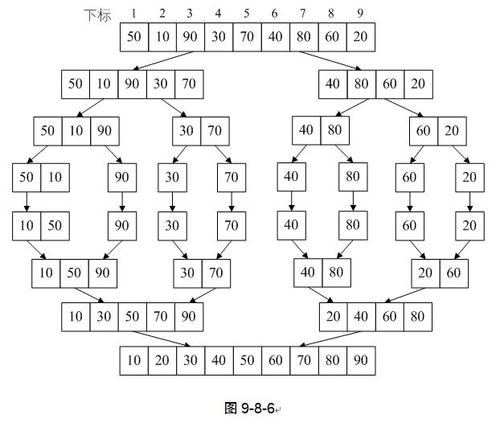
function branch(arr, start = 0, end = arr.length - 1) {
if (end <= start) return
let mid = parseInt((start + end) / 2)
branch.call(this, arr, start, mid)
branch.call(this, arr, mid + 1, end)
mergeSort.call(this, arr, start, mid, end)
}
function mergeSort(arr, start, mid, end) {
let temp = new Array()
let [i, j] = [start, mid + 1]
do {
if (arr[i] <= arr[j]) {
temp.push(arr[i++])
} else {
temp.push(arr[j++])
}
} while (i <= mid && j <= end);
while (i <= mid) {
temp.push(arr[i++])
}
while (j <= end) {
temp.push(arr[j++])
}
for (let k = 0; k < temp.length; k++) {
arr[start + k] = temp[k];
}
}归并的思想理解起来不难,但用js实现起来相对复杂,需要有耐心地理解。
在用js实现这些排序算法的逻辑的过程中,会发现,简单的实现逻辑不是完美的,要考虑性能优化。
是否要改变源数组?如果不改变,那就会产生一个新数组,等于一块临时的内存地址,空间复杂度就会变大;
同理,核心的代码部分,如果是通过产生几个临时变量来辅助存放,那么实现逻辑是很简单的,但是增加了空间复杂度,特别是对于需要递归的算法来说,一旦数据量大就容易造成内存溢出。
实现了一遍之后,再不断地优化自己写的代码,我个人觉得这更有意义。